Use Polar Coordinates Describe Level Curves
From algebra you need fluency with group theory and multilinear algebra including bilinear and Hermitian forms and tensor products. Graph functions plot points visualize algebraic equations add sliders animate graphs and more.
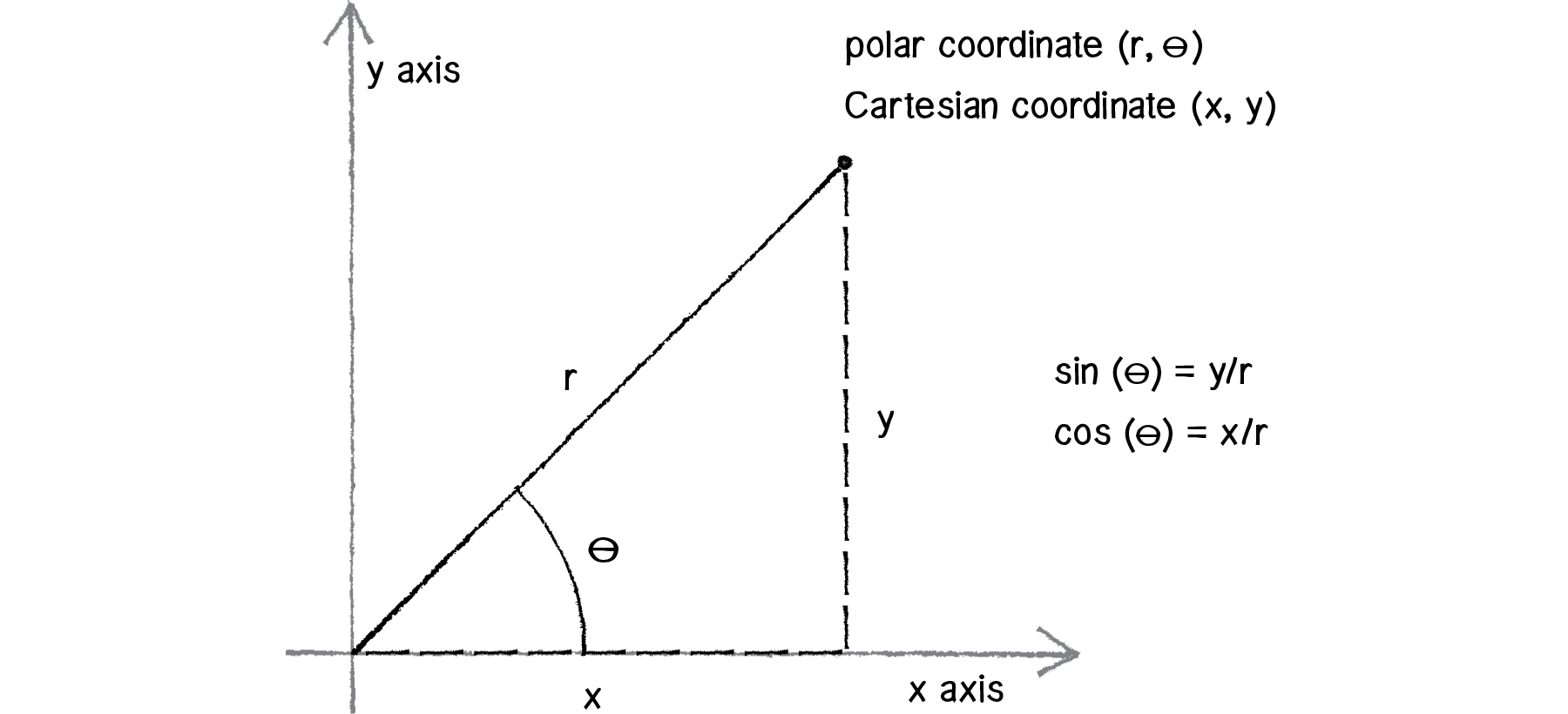
Polar Coordinates Article Khan Academy
The course covers techniques of integration including integration by parts partial fractions improper integrals applications of integration representing functions by infinite series convergence and divergence of series parametric curves and polar coordinates.
. Describe the concept of environmental carrying capacity in the logistic model of population growth. We can help you reach your academic goals hassle-free. We can help you reach your academic goals hassle-free.
Weve Got Your Back. Calculus Volume 2. This is essentially the same thing as when we used polar coordinates in the -plane except we are replacing by Consequently the limits of integration change and we have by using.
Now use the polar substitution and in the -plane. Area and Arc Length in Polar Coordinates. We evaluated the area of a plane region R by iterated integration where the bounds were from curve to curve then from point to point Theorem 1462 allows us to find the volume of a space region with an iterated integral with bounds from surface to surface then from curve to curve then from point to point In the iterated integral.
32 The Logistic Equation Learning Objectives. Origin features easy-to-use templates to display data and functions in polar coordinates including radar and windrose diagrams. Enter the email address you signed up with and well email you a reset link.
Since this vector can be used to define how a particle at a point is changing we can also use it to describe how x andor y is changing at a point. The y coordinate is the northing and the x coordinate is the easting. Power up Your Study Success with Experts Weve Got Your Back.
There is still a small. A short summary of this paper. C- or better in MATH-181 or MATH-173 or 1016-282 or MATH-171 and MATH-180 or.
37 Full PDFs related to this paper. The gradient vectors are perpendicular to the level curves and the magnitudes of the vectors get larger as the level curves get closer together because closely grouped level curves indicate the graph is steep and the magnitude of the gradient vector is the largest value of the directional. In this way we will know that x is increasing twice as fast as y is.
Order Now Order Now. Cambridge International AS and A Level Biology Coursebook Fourth Edition. Cambridge International Biology Course Book 2003.
Isaac Newton described it as a force by which bodies are drawn or impelled or in any way tend towards a. No Galois theory will be needed only a tiny bit of commutative algebra and nothing with a ground field other than the real or. Draw a direction field for a logistic.
First understanding direction fields and what they tell us about a differential equation and its solution is important and can be introduced without any knowledge of how to solve a differential equation and so can be done here before we get into solving them. Section 1-2. Explore math with our beautiful free online graphing calculator.
The simplest example of a coordinate system is the identification of points on a line with real numbers using the number lineIn this system an arbitrary point O the origin is chosen on a given lineThe coordinate of a point P is defined as the signed distance from O to P where the signed distance is the distance taken as positive or negative depending on which side of the. Full PDF Package Download Full PDF Package. Power up Your Academic Success with the Team of Professionals.
They describe measured positions by ordered pairs expressed in northings and eastings or y- and x- coordinates. Well send you the first draft for approval by at. Figure 611 shows the level curves of this function overlaid on the functions gradient vector field.
A centripetal force from Latin centrum center and petere to seek is a force that makes a body follow a curved pathIts direction is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Despite the fact that the assumption of a flat Earth is fundamentally wrong calculation of areas angles and lengths using latitude and longitude can be complicated so plane coordinates persist. For our example we will say that we want the rate of change of f in the direction of vec v leftlangle 21 rightrangle.
Use polar coordinates to find the volume of the given solid bounded by the paraboloid z 6 2x2 2y2 and the plane z 12 in the first octant. Polar graphs are also useful for intuitive visualization of multivariate data. This topic is given its own section for a couple of reasons.
We will use deRham coholomogy a little bit but you could get by with just a high-level understanding of it. Introduction to Differential Equations. Use polar coordinates to find the volume of the given solid bounded by the paraboloid z 6 2x2 2y2 and the plane z 12 in the first octant Create an account to start this course today.
Providing professional development for teachers HMH offers professional learning courses coaching and consulting that is centered on student outcomes. Polar and radial graphs are relevant to any phenomena characterized by its direction and distance from a fixed point for example temperature distribution in Earths Polar Regions.

Definition Of Polar Coordinates R And Unit Vectors E R E Download Scientific Diagram
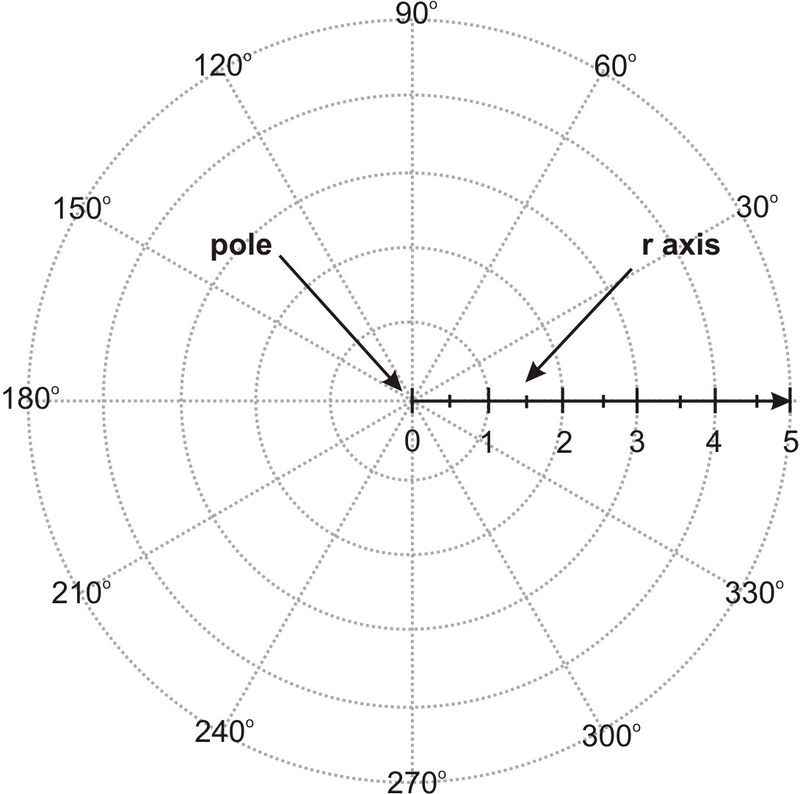
Polar Coordinates Ck 12 Foundation
11 4 Area And Arc Length In Polar Coordinates Mathematics Libretexts

No comments for "Use Polar Coordinates Describe Level Curves"
Post a Comment